---

Atomkerne sind positiv geladen und stoßen sich ab. Die dabei wirkende Kraft heißt Coulomb-Kraft; sie ist umso größer je kleiner der Abstand zwischen den Kernen ist. Wenn sich dennoch zwei Atomkerne auf den Abstand weniger Kernradien annähern, wirkt zusätzlich eine anziehende Kraft. Sie ermöglicht die Fusion. Die beiden Atomkerne können sich nur dann hinreichend nahekommen, wenn sie sich mit großen Geschwindigkeiten aufeinander zu bewegen. Diese Situation ist einem Automobil vergleichbar, das im Leerlauf auf einen immer steiler werdenden Berg hinaufrollen soll. Die Spitze des Berges, also Fusion, wird nur dann erreicht, wenn das Auto am Fuß des Berges genügend Schwung, also Geschwindigkeit, hatte. In einem Gas oder einem Plasma bewegen sich die Atome bzw. Atomkerne unabhängig voneinander und es interessiert nur der Durchschnitt aller Geschwindigkeiten. Haben beispielsweise die Teilchen im Mittel eine hohe Geschwindigkeit, so spricht man auch von hoher Temperatur (angegeben in Grad Kelvin, K) oder großer hoher Bewegungsenergie (angegeben in Elektronenvolt, eV, wobei 1 eV=1,16⋅10⁴ K=1,6⋅10^-19 Joule). Die für die Fusion notwendigen Geschwindigkeiten der Atomkerne werden nur in Plasmen hoher Temperatur oder in Teilchenbeschleunigern erreicht.

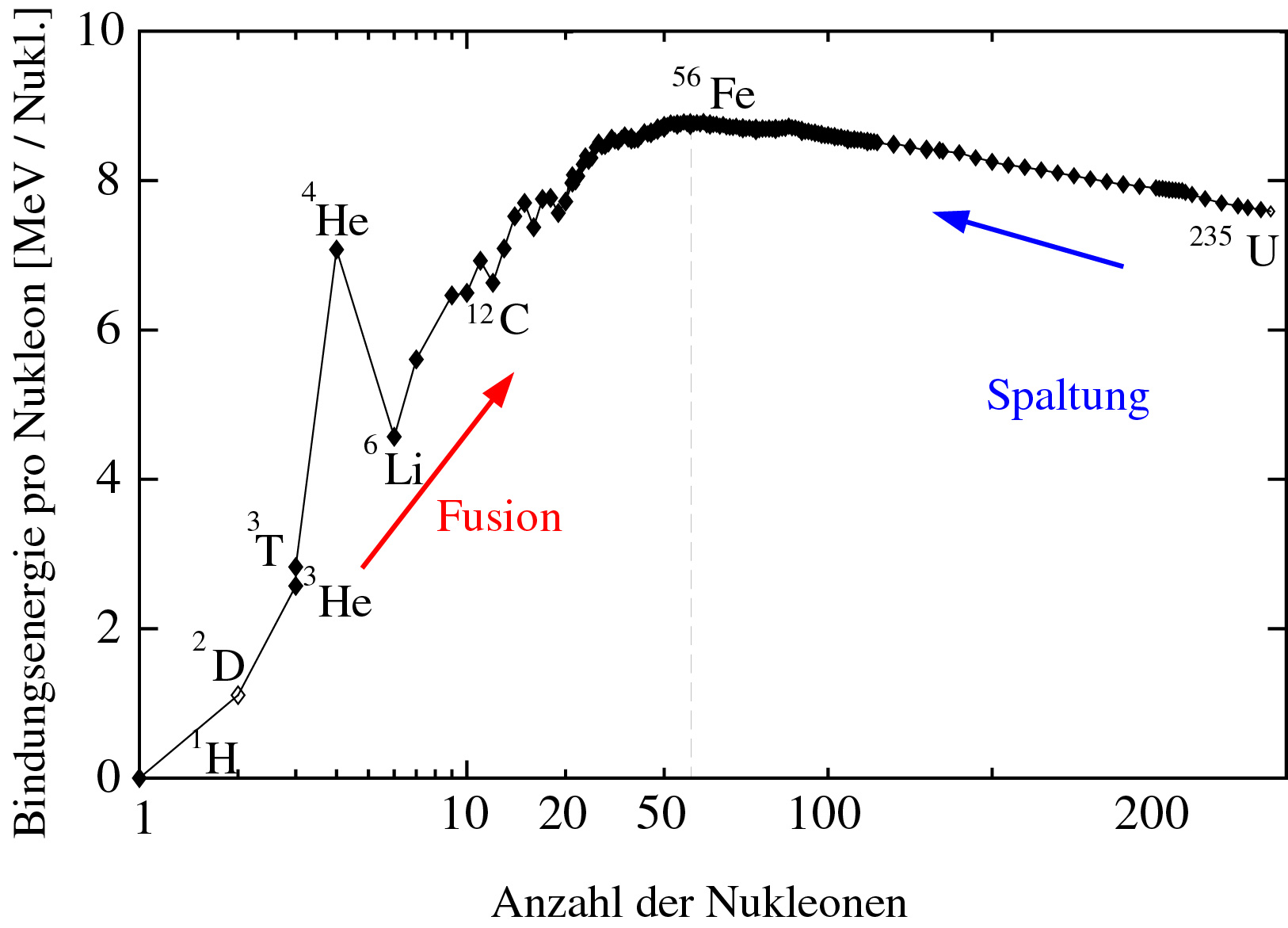
Atomkerne bestehen aus positiv geladenen Protonen und neutralen Neutronen. Beide Bestandteile heißen Nukleonen. Im allgemeinen ist die Masse eines Atomkerns kleiner als die Gesamtmasse seiner Nukleonen. Diese Massendifferenz, m, wird nach Albert Einsteins berühmter Formel, E=m⋅c², (c ist die Lichtgeschwindigkeit) bei der Entstehung eines Atomkernes aus den Nukleonen in die Energie, E, umgewandelt und als Bewegungsenergie (Geschwindigkeit) freigesetzt oder als elektromagnetische Welle abgestrahlt. Diese Energie heißt Bindungsenergie. In Abb. 1 ist die im Mittel pro Nukleon freigesetzte Bindungsenergie für verschiedene Elemente aufgetragen. Eisen hat die höchste Bindungsenergie pro Nukleon, d.h. bei seiner Entstehung wurde am meisten Energie freigesetzt. Leichtere Elemente, wie Wasserstoff, oder schwerere Elemente, wie Uran, haben eine geringere Bindungsenergie. Daher wird Energie frei, wenn schwere Elemente gespalten werden und leichtere Elemente entstehen. Diese Kernreaktion ist die Grundlage der Spaltungsreaktoren, kurz: der Atomreaktoren. Im umgekehrten Fall, wenn aus Kernen, wie dem Wasserstoff, durch Fusion schwerere Kerne gebildet werden, wird auch Energie frei. Besonders deutlich ist der Unterschied in der Bindungsenergie pro Nukleon zwischen den beiden Wasserstoffisotopen Deuterium, D, (ein Proton und ein Neutron) oder Tritium, T, (ein Proton und zwei Neutronen) und Helium, ⁴He. Der Prozess, bei dem diese beiden Wasserstoffisotope zu Helium verschmelzen, soll die Grundlage zukünftiger Fusionsreaktoren werden.

Kernfusion ist die Grundlage der Energieerzeugung in Sternen, wie auch in unserer Sonne. Die dabei freigesetzte Energie wird als elektromagnetische Strahlung in das Weltall abgestrahlt und macht Leben auf der Erde erst möglich. Über Jahrmillionen wurde ein kleiner Teil dieser Energie über photosynthetische Prozesse gespeichert und steht als fossiler Brennstoff zur Verfügung. Das Verbrennen von fossilen Brennstoffen ist eine chemische Reaktion; es treten hier nur Veränderungen in der Elektronenhülle der beteiligen Elemente und Moleküle auf, die Atomkerne selbst ändern sich nicht. Die dabei freigesetzte Energie ist etwa 1 Million mal kleiner als in Kernreaktionen. Das bedeutet zum Beispiel, dass etwa 1000 t Kohle verbrannt werden müssten, um die gleiche Energie zu erzeugen, die man durch atomares "Verbrennen", also Verschmelzen, von 1 kg Wasserstoff erreichen könnte.

Die Sonne besteht fast vollständig aus einem Plasma aus einfachem Wasserstoff (Protonen). In einem sehr langsam ablaufenden Prozess verschmelzen die Protonen miteinander unter Freisetzung von Energie. Dabei werden immerhin pro Sekunde werden 600 Mio. t Wasserstoff zu 595 Mio. t Helium verbrannt. Das entspricht der Leistung von etwa 2⋅10¹⁶ Atomkraftwerken. Dennoch reicht der übrige Wasserstoff aus, um die Sonne für weitere 4 Mrd. Jahre zu betreiben. Da auch auf der Erde Wasserstoff praktisch unbegrenzt zur Verfügung steht, entwickelten sich schon bald Bemühungen, hier ähnliche Bedingungen zu schaffen, wie sie in der Sonne herrschen. In unkontrollierter Form gelang dies 1952 in der Wasserstoff-Bombe, wo durch Zündung einer Atombombe kurzzeitig die notwendig hohen Temperaturen und Dichten erreicht wurden, unter denen Wasserstoff teilweise zu Helium fusionierte. Kontrollierte Kernfusion aber stellte sich als große wissenschaftliche Herausforderung heraus und bald war klar, dass das Ziel und damit die verbundenen wirtschaftlichen Vorteile nicht schnell erreicht werden können. Daher wurde die anfängliche Geheimhaltung 1958 teilweise aufgegeben und es wird seit dieser Zeit mit zunehmender internationaler Verflechtung daran gearbeitet.

Bei den für Kernfusion notwendig hohen Temperaturen liegt Wasserstoff als Plasma vor, das heißt, die Atome sind aufgebrochen und Elektronen und Wasserstoffkerne bewegen sich unabhängig voneinander. Ein wichtiges Ziel der Fusionsforschung ist es, Methoden zu entwickeln, das Plasma einzuschliessen. In den Sternen wird das Plasma durch Gravitation zusammengehalten. Auf der Erde steht diese Möglichkeit nicht zur Verfügung, da die Plasmen zu klein sind. Direkter Einschluss in Gefäßen ist nicht möglich, da das Plasma durch den Kontakt zur Wand zu schnell abkühlen würde. Doch gibt es zwei Möglichkeiten, das Plasma ohne Wandkontakt einzuschließen. Beim magnetischen Einschluss werden die Elektronen und Protonen durch Magnetfelder auf Schraubenbahnen um die Magnetfeldlinien gelenkt, wodurch ihre Ausbreitung senkrecht dazu reduziert wird. Beim Trägheitseinschluss wird durch intensive Laser- oder Teilchenstrahlung eine Wasserstoffkapsel sehr schnell auf Fusionstemperaturen und -dichten gebracht, so dass in der Zeit, in der das Plasma expandiert, bereits ausreichend viele Fusionsreaktionen stattfinden.

Kernfusion ist auch möglich, wenn in Wasserstoff das Elektron der Hülle, durch das 270 mal schwere Elementarteilchen Myon ersetzt wird. Dann ist das Wasserstoffatom kleiner und das Myon schirmt die abstoßende Coulomb-Kraft der Kerne bis auf genügend kurze Distanzen ab. Schließlich treten Kernfusionsreaktionen auch in dem Querschnitt aufeinander gerichteter hochenergetischer Teilchenstrahlen auf. In der Grundlagenforschung werden in solchen Anordnungen die Reaktionswahrscheinlichkeiten untersucht und die Reaktionsprodukte bestimmt. Sie sind aber für die Anwendung in einem Fusionsreaktor unwirtschaftlich, da die bei der geringen Anzahl an Kernreaktionen freigesetzte Energie zu klein ist im Vergleich zu der Energie, die aufgewandt werden muss, die Teilchenstrahlen zu erzeugen.

Die Wahrscheinlichkeit, dass zwei Wasserstoffkerne miteinander verschmelzen, ist abhängig von den beteiligten Isotopen und deren Temperatur. Bekannte Reaktionen sind

D   +   T   →   ⁴He (3,5)   +   n (14)

D   +   D   →   T (1)   +   p (3)

D   +   D   →   ³He (0,8)   +   n (2,5)

D   +   ³He   →   ⁴He (3,7)   +   p (14,7).

Die pro Kernreaktion freigesetzte Energie ist in MeV in Klammern angegeben. Dabei verteilt sich die Gesamtenergie auf die Reaktionsprodukte wegen Impulserhaltung umgekehrt proportional zu den Massen. Gibt man ein Plasma mit festem Druck vor, d.h. ist das Produkt aus Teilchendichte und Temperatur konstant, so ist die erste Reaktion die geeigneteste für einen Fusionsreaktor. Nicht nur hat ihre Fusionsleistung ein Maximum bei einer kleineren Temperatur als die anderen Reaktionen; diese Fusionsleistung ist auch um fast einen Faktor 100 größer als das Maximum der anderen Reaktionen. Leider entstehen bei dieser Reaktion Neutronen, die nicht im Plasma eingeschlossen werden und die Strukturmaterialien aktivieren können. Außerdem muss radioaktives Tritium verwendet werden. Sämtlichen Reaktionen ist gemeinsam, dass sie viel schneller ablaufen als die stellaren Reaktionen, in denen einfacher Wasserstoff verbrannt wird. Wären sie die Grundlage der Energieproduktion der Sterne gewesen, wären die Sterne mittlerweile längst ausgebrannt.

Im allgemeinen befinden sich Plasmen und besonders Fusionsplasmen nicht im thermischen Gleichgewicht mit ihrer Umgebung, d.h. die Plasmatemperatur, T, nimmt mit der Zeit ab, wenn die plasmaerzeugende Quelle abgeschaltet wird. Diese Abklingzeit wird als Energieeinschlusszeit, τ_E, bezeichnet. Eine lange Energieeinschlusszeit bedeutet beispielsweise, dass das Plasma gut von seiner Umgebung isoliert ist und nur langsam auskühlt. Die Neutronen, die bei obiger DT-Reaktion entstehen, verlassen das Plasma ohne Wechselwirkung mit 80% der Reaktionsenergie; dagegen kann das α-Teilchen, ⁴He, seine Energie an das übrige Plasma durch Stöße abgeben. Man spricht von Plasmazündung, wenn sich das Plasma selbst aufrechterhalten kann. Das ist der Fall, wenn die durch α-Teilchen-Heizung pro Zeiteinheit zugeführte Energie größer ist als der entsprechende Energieverlust. Für Zündung muss das Plasma auch bei der DT-Reaktion immer noch eine Temperatur, T, von etwa 10 keV, das entpricht 100 Mio. °C, haben. Der Energieverlust setzt sich zusammen aus Verlusten durch elektromagnetische Strahlung (Bremsstrahlung) und unerwünschtem Entweichen des Plasmas aus dem Einschlussbereich. Unter Berücksichtigung der Temperaturabhängigkeit der DT-Reaktion erhält man als Zündbedingung für das Plasma

n⋅τ_E > 2⋅10²⁰ m^-3s bei T=10 keV

darin ist n die Teilchendichte der Protonen. Sowohl bei niedrigeren wie auch bei höheren Temperaturen ist der Mindestwert des Produktes aus Dichte und Einschlusszeit größer. Das Ziel der Fusionsforschung ist es, Plasmen auf Temperaturen von etwa 10 keV aufzuheizen und mit ausreichend hoher Dichte und Energieeinschlusszeit zu erhalten, auf dass das Produkt den angegebenen Wert übersteigt. Bei dem Trägheitseinschluss ist die Energieeinschlusszeit durch die sehr kurze Expansionszeit des Plasmas gegeben und es wird daher versucht, die Dichte entsprechend zu erhöhen. Typische Werte sind Teilchendichten von etwa 10³¹m^-3 und Einschlusszeiten von einigen 10^-11 s. Beim magnetischen Einschluss findet man, dass die Teilchendichte sich nicht beliebig erhöhen lässt und man versucht daher, die Energieeinschlusszeit zu verbessern. Hier ist die Zündbedingung gar noch etwas stringenter, da zusätzlich berücksichtigt werden muss, dass das entstehende Helium den Plasmabrennstoff verdünnt und erodierte Strukturmaterialen das Plasma verunreinigen und durch Strahlung den Energieverlust erhöhen. Typische Werte sind Teilchendichten von 10²⁰m^-3 (weniger als 0.001% der Teilchendichte von Luft bei Atmosphärendruck) und Energieeinschlusszeiten von einigen Sekunden. Der Ausdruck n⋅τ_E wird auch als Fusionsprodukt bezeichnet. Er wird vielfach dargestellt, um die Fortschritte bei verschiedenen Experimenten vergleichen zu können.

Ein Fusionsreaktor arbeitet erst dann energetisch wirtschaftlich, wenn die produzierte, thermische Leistung, P_f, ein Vielfaches der Leistung, P_h, ist, die für Plasmaheizung aufgewendet werden muss. Dies wird mit dem Q-Faktor beschrieben, Q = P_f / P_h, der natürlich sehr viel größer als 1 sein soll. breakeven wird der Zustand bezeichnet, wenn Q=1, d.h. die aufgewendete Fremdleistung gleich der Fusionsleistung ist. In einem voll gezündeten Plasma ist Q unendlich. Da Tritium radioaktiv ist, wird in vielen Experimenten mit magnetischem Einschluss nur mit Deuterium gearbeitet. Für solche Plasmen errechnet man ein äquivalentes Q, das man bei sonst gleichen Bedingungen mit einem DT Gemisch erhalten hätte. Mittlerweile wurde bei tatsächlichem DT –Betrieb Q=1 für magnetischen Einschluss nahezu erreicht.

→ Was ist Kernfusion?
→ Zur gesteuerten Kernfusion.