---

In einem Magnetfeld bewegen sich Elektronen und die Ionen auf Schraubenbahnen entlang der Magnetfeldlinien, deren Durchmesser mit zunehmendem Magnetfeld kleiner wird. Bei einem typischen Magnetfeld von 2 Tesla und einer Plasmatemperatur von 5 keV haben Ionen einen Bahndurchmesser von 5 mm und Elektronen von 0.1 mm. Dadurch ist die Beweglichkeit quer zum Magnetfeld stark eingeschränkt und eine gute Isolation des Plasmas von den seitlichen Gefäßwänden ist möglich. Jedoch kann das Plasma immer noch entlang des Feldes entweichen. Stärkere Magnetfelder an den Enden können den Plasmaeinschluss verbessern, da dann ein großer Anteil der Plasmateilchen von den stärkeren Endfeldern reflektiert wird. Solche Experimente heißen Spiegelmaschinen. Ein besseres Einschlussverhalten wird mit ringförmig geschlossenen Magnetfeldern erreicht. Die denkbar einfachste Anordnung entsteht, indem man eine lange gerade Spule zu einem Ring verformt. Das eingeschlossene Volumen hat die Form eines Torus. Weiterhin bewegen sich die Elektronen und Ionen entlang des Magnetfeldes auf Schraubenbahnen, doch führt die Krümmung der Magnetfeldlinien zu einer zusätzlichen, vertikalen Driftbewegung. Da diese für die Elektronen und Ionen eine unterschiedliche Richtung hat, kommt es zur Ladungstrennung und es baut sich im Plasmainnern ein elektrisches Feld auf. Dieses Feld katapultiert das Plasma quer zum Magnetfeld aus dem Einschlussbereich. Eine deutliche Verbesserung kann dadurch erreicht werden, dass die Magnetfeldlinien selbst schraubenförmig verdreht sind. Damit kommen die Teilchen auf ihrer Bahn abwechselnd in den oberen oder unteren Plasmabereich und die weiterhin vertikale Driftbewegung führt dazu, dass die Drift abwechselnd zum Plasmazentrum oder zum Plasmarand gerichtet ist und sich kompensiert.

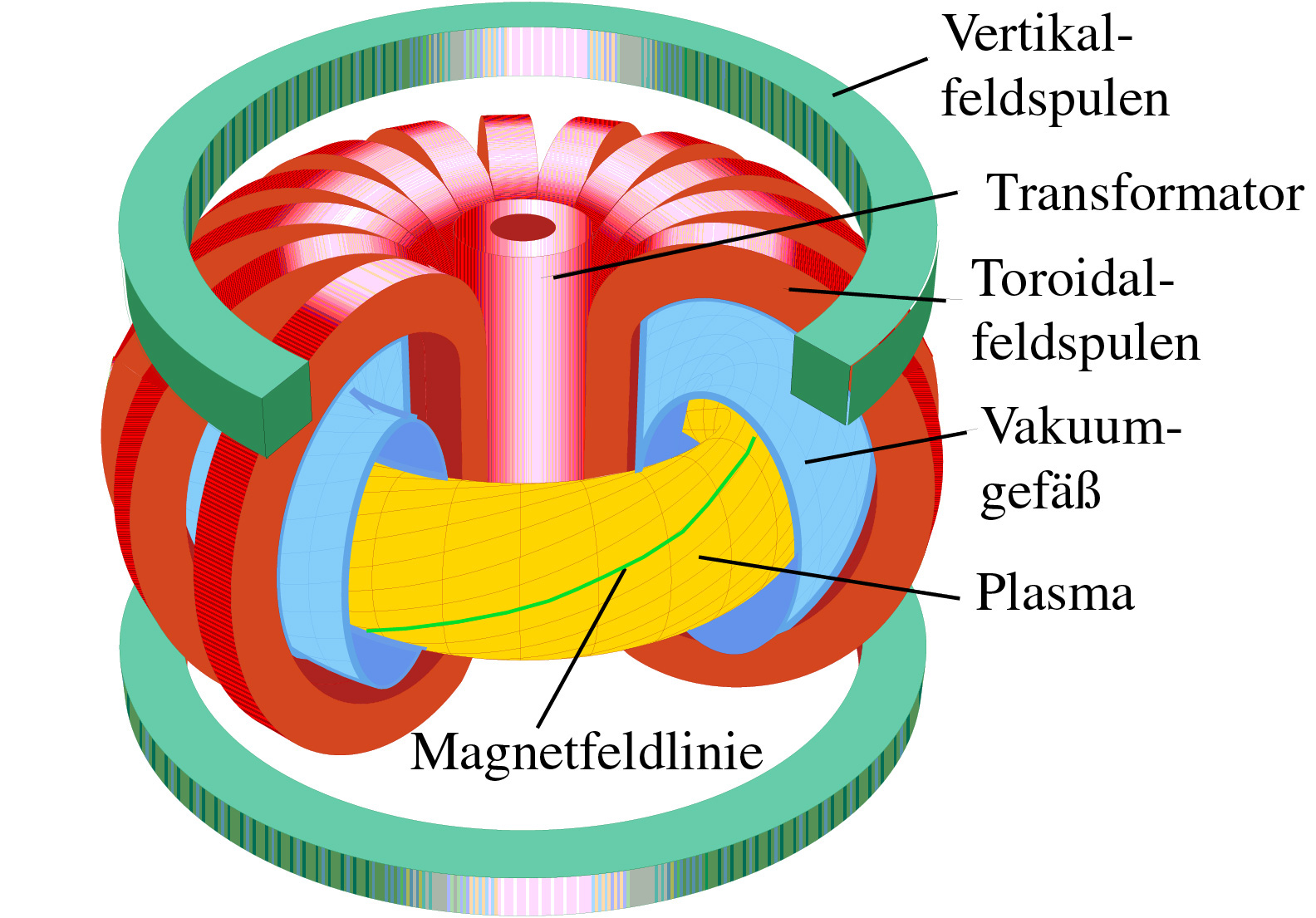
Abb.1 Schematische Darstellung eines Tokamaks.

Prinzipiell gibt es zwei Möglichkeiten, ein verschraubtes, in sich selbst geschlossenes Magnetfeld zu erzeugen. Ein Tokamak (russ. für "toroidale Kammer in einer Magnetfeldspule") besteht aus dem oben beschriebenen einfachen, toroidalen Magnetfeld. Zusätzlich wird in dem torusförmigen Plasma ein Ringstrom induziert, wobei das Plasma die Sekundärwicklung eines Transformators darstellt. Das poloidale Magnetfeld dieses Stromes überlagert das von äußere toroidale Magnetfeld mit dem Ergebnis einer Verschraubung des Gesamtfeldes. Abb. 1 zeigt den schematischen Aufbau eines Tokamaks. Ein Beispiel für einen Tokamak ist ASDEX-Upgrade (Axisymmetrisches Divertor Experiment) in Garching. Der eingeschlossene Plasmaring hat dort einen Durchmesser von 3,3 m und eine mittlere Dicke von 1,3 m. Abb. 2 zeigt einen Blick in das Torusinnere von ASDEX-Upgrade während einer Montagephase.

Abb. 2 Blick in den Torus von ASDEX-Upgrade.

In einem Stellarator (lat. stella, Stern) wurde das verschraubte Magnetfeld zunächst durch das Toroidalfeld und zusätzliche helikale Spulen erreicht. Genauer spricht man daher auch von helikalen Systemen. Dadurch sind in einem Stellarator - im Gegensatz zu einem Tokamak - Magnetfeld und Plasmaform nicht mehr axialsymmetrisch. Seit einigen Jahren ist es aber mit zunehmender Rechnerleistung möglich geworden, toroidale und helikale Spulen auch zu kombinieren und nichtplanare, modulare Spulen zu konstruieren. Dabei eröffnet sich die Möglichkeit, die Magnetfelder für guten Plasmaeinschluss und weitere Eigenschaften, wie z. B. die Empfindlichkeit, mit der ein Plasma auf Störungen reagiert, zu optimieren. Das Magnetfeld des Stellarators Wendelstein 7-X, der gegenwärtig in europäischem Verbund in Greifswald gebaut wird, ist das Produkt eines solchen Optimierungsprozesses. Abb. 3 zeigt die Magnetfeldspulen von W7-X und das Plasma. Deutlich ist die dreidimensionale Form des Plasmas zu erkennen. Der Durchmesser des Plasmaringes beträgt 11 m, die mittlere Dicke des Plasmas beträgt etwa 1,1 m.

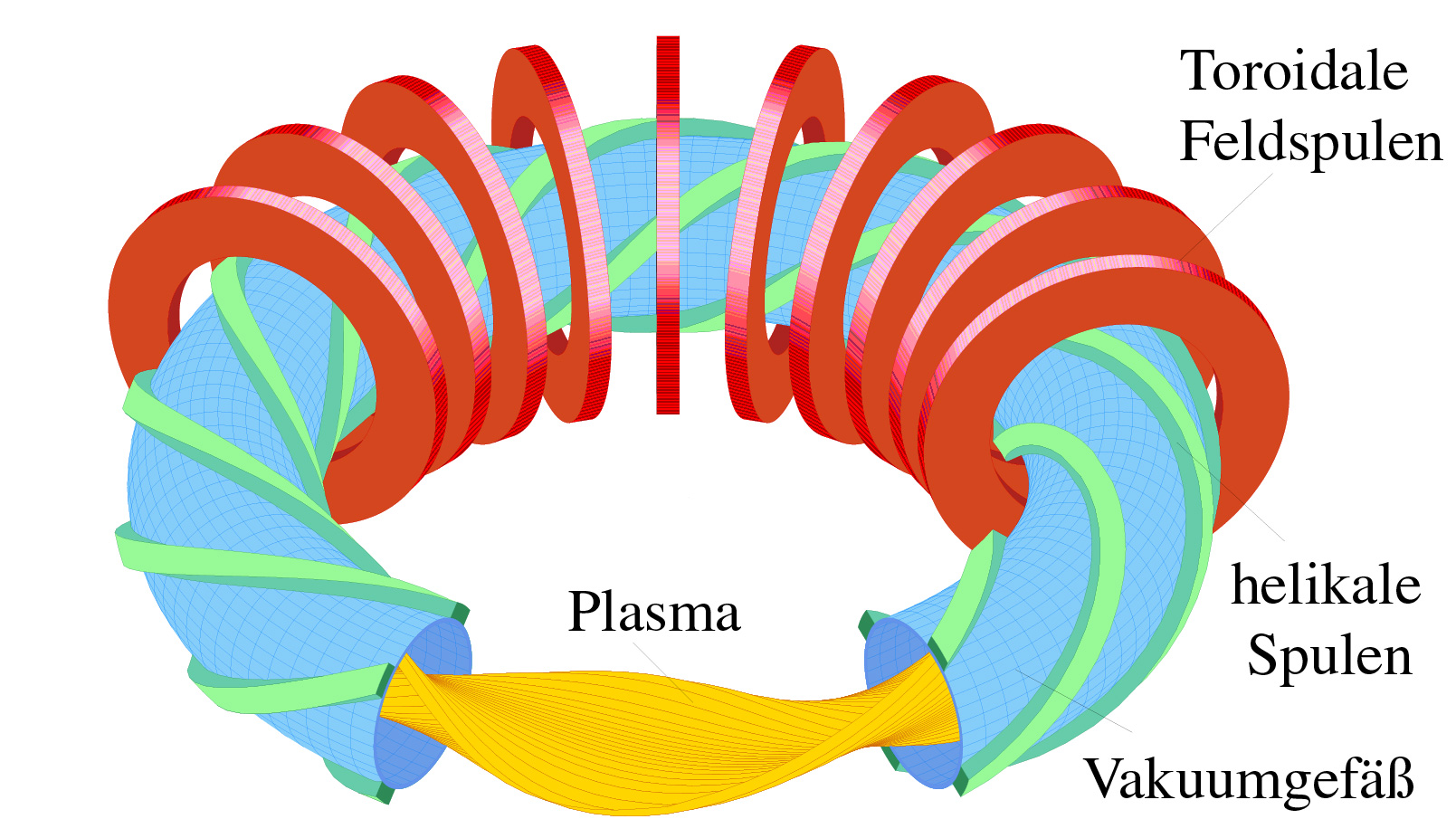
Abb. 3 Schematische Darstellung des Stellarators W7-X.

Neben diesen beiden, favorisierten magnetischen Einschlussverfahren, gibt es weitere, wie z.B. den Spheromak, bei dem das Plasma nicht Ring- sondern nahezu Kugelform hat und ein Strom im Plasma selbst das toroidale Magnetfeld erzeugt. Diese alternativen Konzepte werden häufig nur in kleineren Experimenten an Universitäten verfolgt und sind Teil der Grundlagenforschung.

Tokamaks und Stellaratoren besitzen unterschiedliche Vorzüge und Nachteile. Tokamakexperimente haben einen wenigstens 15jährigen Entwicklungsvorsprung vor Stellaratoren. Sie haben auch den Vorteil eines einfachen Aufbaus. Doch ist Plasmaeinschluss nur möglich, solange im Plasma ein Ringstrom fließt. Da der Stromhub auf der Primärseite des Transformators begrenzt ist, denn dort wird während des Betriebs der Strom kontinuierlich verändert, kann ein Tokamak eigentlich nur gepulst betrieben werden. Doch erregt ein Plasma in toroidaler Anordnung bereits selbst einen ringförmigen Plasmastrom und zusätzlicher Strom kann auch mit eingestrahlten Radiowellen oder durch Teilcheneinschuss getrieben werden; somit sind Plasmapulslängen von Stunden denkbar. In kleinen Experimenten wurden 120 Minuten bereits erreicht. Unter bestimmten Plasmabedingungen allerdings kann der Ringstrom im Plasma abreissen. Dabei wirken auf den Torus und seine Einbauten große Kräfte, die zu Beschädigungen führen können. Das frühzeitige Erkennen solcher Bedingungen und das Einleiten von Gegenmaßnahmen sind zunehmend Gegenstand der aktuellen Forschung. Trotzdem besitzt der Tokamak Eignung als Reaktorkonzept. Im Gegensatz dazu erfordern Stellaratoren komplizierte Geometrien, die Aufbau und Wartung erschweren, sind aber prinzipiell für kontinuierlichen Betrieb geeignet, da das äußere Magnetfeld bereits das Plasma einschließt. Der selbsterregte Plasmastrom ist gering und wurde für W7-X durch die Optimierung so weit reduziert, dass die Gefahr eines Stromabrisses nicht existiert.

Tokamaks und Stellaratoren benötigen zusätzliche Heizungen, um das Plasma auf die zur Zündung erforderlichen Temperaturen zu bringen. Tokamaks haben bereits eine inhärente Heizung durch den Plasmastrom. Diese Art der Heizung entspricht der einer Glühwendel, doch nimmt im Plasma die Resistivität im Gegensatz zu der Glühwendel mit zunehmender Temperatur ab, so dass damit maximal eine Temperatur von wenigen keV erreicht werden kann. Heizung auf noch höhere Temperaturen ist möglich durch den Einschuss neutraler Wasserstoffatome mit hoher Energie. Wegen ihrer Neutralität können diese quer in das Magnetfeld eindringen, werden dann im Plasma ionisiert und damit eingeschlossen und geben schließlich ihre Energie durch Stöße an das übrige Plasma ab. Erzeugt werden diese hochenergetischen Wasserstoffatome, indem aus einer Plasmaquelle Wasserstoffionen zuerst durch elektrische Felder extrahiert und mit weiteren elektrischen Feldern von 50.000 bis 1 Mio. Volt beschleunigt werden. Durch anschließende Wechselwirkung mit Wasserstoffgas findet eine Neutralisation der Wasserstoffionen statt. Zusatzheizung ist auch möglich durch resonante Absorption elektromagnetischer Wellen durch Ionen oder Elektronen bei Frequenzen von einigen 10 MHz bis 200 GHz. Die eingestrahlten Wellen werden dann besonders gut absorbiert, wenn ihre Frequenz mit der Rotationsfrequenz der Ionen oder Elektronen um die Magnetfeldlinien übereinstimmt. Diese Art der Heizung ist ähnlich zu der eines Mikrowellenofens im Haushalt.

Ein Hauptziel der Forschung an magnetischem Einschlussverfahren ist es, Magnetfeldkonfigurationen oder Plasmazustände zu finden, die die Energieeinschlusszeit verlängern, um die Zündbedingung erfüllen zu können. In den meisten Experimenten ist die experimentell gemessene Energieeinschlusszeit viel kürzer als theoretisch erklärt werden kann. Sie ist bestimmt dadurch, dass sich das Plasma durch Stöße zwischen den Teilchen auch quer zum Magnetfeld ausbreiten kann. Diese Ausbreitungsgeschwindigkeit ist größer als erwartet und noch nicht vollständig verstanden. Doch zeigen viele Experimente (Tokamaks wie Stellaratoren) gleiche Abhängigkeiten der gemessenen Energieeinschlusszeit von Dichte, Temperatur, Magnetfeld, Torusdurchmesser und Plasmaradius. Aus diesen Abhängigkeiten hat man schon früh richtig gefolgert, dass das Plasma in größeren Anordnungen besser eingeschlossen ist. Für das Plasma bedeutet das vereinfacht, dass bei gegebener Geometrie maximal eine bestimmte Gesamtenergie gespeichert werden kann. Wird das Plasma aufgeheizt, verhält es sich dabei ganz ähnlich wie ein Sandhaufen, der in der Mitte eines Tisches durch Beschüttung errichtet werden soll. Die Spitze des Sandhaufens entspricht in diesem Model der Maximaltemperatur des Plasmas im Zentrum. Mit zunehmender Beschüttung (Heizung) nimmt die Höhe des Sandhaufens zu, doch führen die sporadisch entstehenden kleinen Sandlawinen dazu, dass die Steigung des Sandhaufens etwa konstant bleibt; damit hat ein Sandhaufen gegebener Breite auch eine bestimmte, maximale Höhe und das Plasma eine Maximaltemperatur. Das bedeutet weiterhin, dass das Plasma eine bestimmte Größe haben muss, um im Zentrum 10 keV zu erreichen. Hoffnung schöpft man aber aus der Beobachtung, dass sich unter bestimmten Umständen die Profile (die Steigung des Sandhaufens) lokal aufsteilen können und sich damit die Gesamtenergie deutlich erhöht. Diese Verbesserungen wurden Anfang der 80er Jahre zum ersten Mal beobachtet. Mittlerweile existiert ein gutes, empirisches Verständnis der Bedingungen, die zu diesen Verbesserungen führen, die Mechanismen selbst sind aber noch nicht verstanden und werden weiterhin detailliert untersucht.

Der konstante Fluss von Plasmateilchen und Energie aus dem Plasmainnern stellt hohe Anforderungen an die Wände des Plasmagefäßes. Die Wandmaterialien dürfen dabei nicht zu sehr abgetragen werden, da sie zum einen das Plasma verdünnen und zum anderen - viel schlimmer - wegen ihrer hoher Kernladungszahl Energie sehr effektiv aus dem Plasmainnern abstrahlen und damit dessen Temperatur erniedrigen. Mit zusätzlichen Magnetfeldern am Rand lässt man daher das ausströmende Plasma unter sehr flachem Winkel auf dafür geeignete, besonders gehärtete Oberflächen, die Prallplatten sogenannter Divertoren, auftreffen. In einem Reaktor müssen diese Oberflächen gut gekühlt werden, um eine auftreffende Leistungsdichte von etwa 1 kW/cm² beständig abführen zu können.

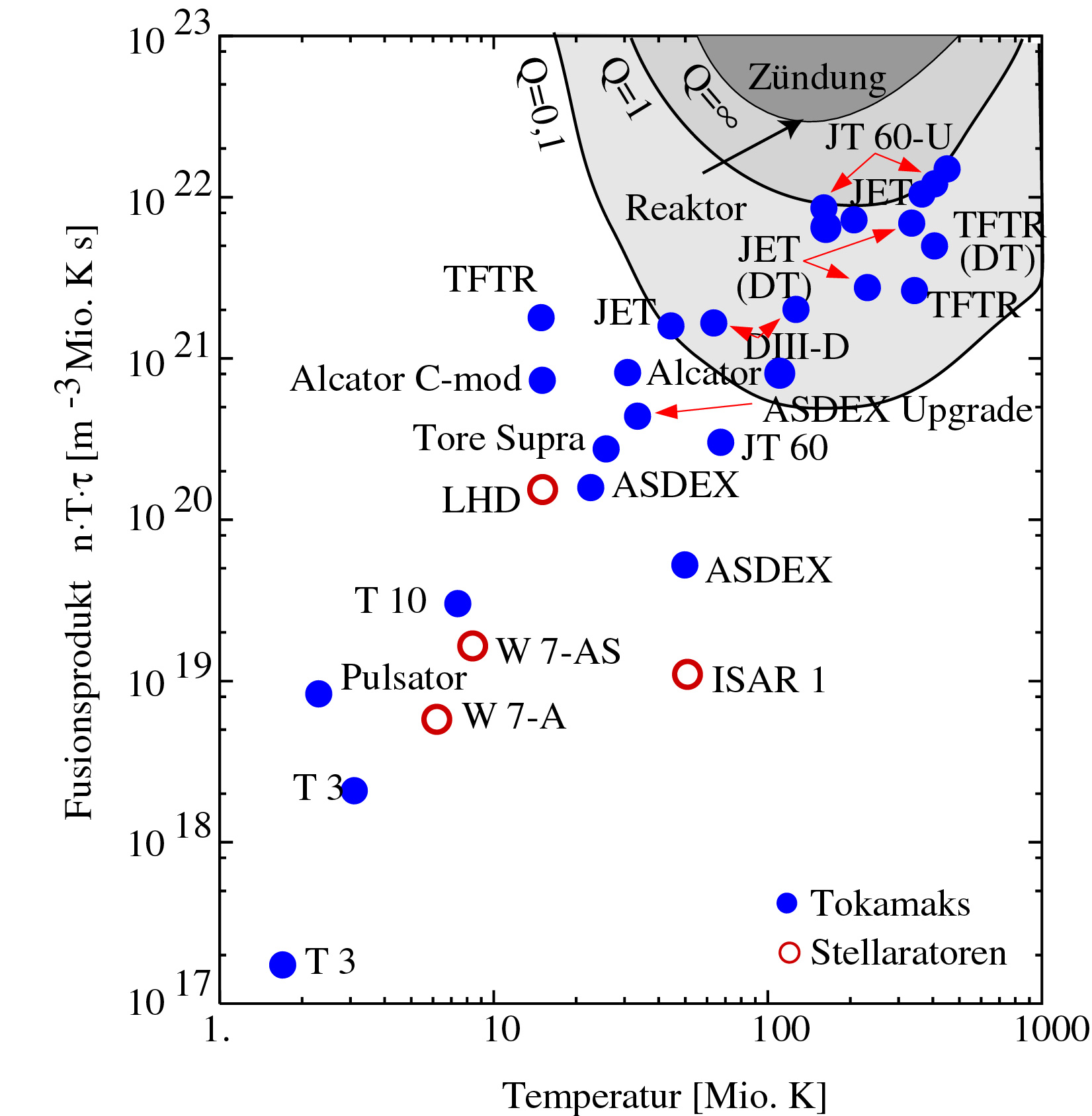
Abb. 4 Erreichte Werte des Fusionsproduktes.

Abb. 4 zeigt die Werte des Fusionsproduktes n× T× t _E, die in verschiedenen Experimenten (Tokamaks und Stellaratoren) bislang erreicht wurden. In Tab. 1 sind einige Eigenschaften der Experimente zusammengestellt: das Jahr des Experimentbeginns, der Radius R des Plasmarings, der Radius a des Plasmas, das Magnetfeld B im Plasmazentrum und die gesamte Zusatzheizung. Der höchste Wert des Fusionsproduktes, 1997 erzielt an JET (Joint European Torus, Culham, einem Projekt der europäischen Gemeinschaft) ist noch etwa einen Faktor 7 von Zündung entfernt. Der niedrigste Wert auf der Abbildung ist von dem ersten Tokamak, T3, von 1968. Damit wurde in drei Jahrzehnten das Fusionsprodukt um einen Faktor von etwa 10.000 verbessert. Die getönten Flächen markieren den Q-Faktor, dem die Plasmabedingungen für ein Deuterium/ Tritium Gemisch entsprechen. Nur zwei Experimente erlaubten Betrieb mit Deuterium und Tritium: JET und TFTR (Tokamak Fusion Test Reactor, Princeton, USA). Bislang wurden Rekordwerte von mehr als 16 MW bzw. 10 MW Fusionsleistung in diesen Experimenten erreicht.

Experiment	Ort	Typ	Jahr	R [m]	a[m]	B [T]	Ph [MW]
T-3	UdSSR	Tokamak	1962	1,0	0,12	2,5	0
T-10	UdSSR	Tokamak	1975	1,5	0,37	4,5	1
ASDEX	D	Tokamak	1980	1,54	0,4	3,0	4
→ JT-60	J	Tokamak	1985	3,0	0,95	4,5	30
→ Alcator	USA	Tokamak	1979	0,64	0,17	12	4
→ TFTR	USA	Tokamak	1982	2,4	0,8	5	51
→ JET	EU	Tokamak	1983	3,0	1,25	3,5	47
→ D-III D	USA	Tokamak	1986	1,7	0,7	2,1	26
→ Tore Supra	F	Tokamak	1988	2,4	0,8	4,5	22
→ ASDEX Upgrade	D	Tokamak	1991	1,7	0,5	3,0	30
→ W7-AS	D	Stellarator	1992	2,0	0,2	2,5	7
→ LHD	J	Stellarator	1998	3,5	0,6	3	11
→ HSX	USA	Stellarator	1999	1,0	0,2	0,5	0,5

Tab. 1 Übersicht über einige Fusionsexperimente. Erklärung der Kürzel im Text.